Particle hydrodynamics
Eulerian-Lagrangian Hybrids
This research aims to develop minimal models to resolve particle hydrodynamics in a robust and quite general way. The novelty resides in the type of coupling between the fluid and the small particles immersed in it, which is based on a "coarse-grained" no-slip constraint which enforces equal particle velocity and local average of fluid velocity within the particle "volume". This non-linear "inertial coupling", permits to consistently solve both, the fluid and particle inertia and conserves momentum and energy. Owing to the non-dissipative nature of the no-slip coupling, the fluctuation-dissipation balance is possible without addition of extra particle noise. Thus, we just take into account thermal fluctuations in the fluid momentum equation, as expressed in the Landau-Lifshitz formalism for fluctuating hydrodynamics. The local averaging and spreading operations are accomplished using compact kernels used in immersed boundary methods. These kernels are soft, so the particle model resembles a "blob" which however has surprisingly physically-consistent volume, mass, and hydrodynamic properties. The present inertial coupling method can model particulate flows in a wide range of time-scales ranging from Brownian to convection-driven motion, using a minimal cost. It can be naturally extended to polymeric fluids and other types of physico/chemical phenomena. In the incompressible formulation, the code is able to reach large particle Reynolds numbers (about 200) and consistently reproduce the increase of fluid drag and transient effects due to particle-wake interaction at large Re.
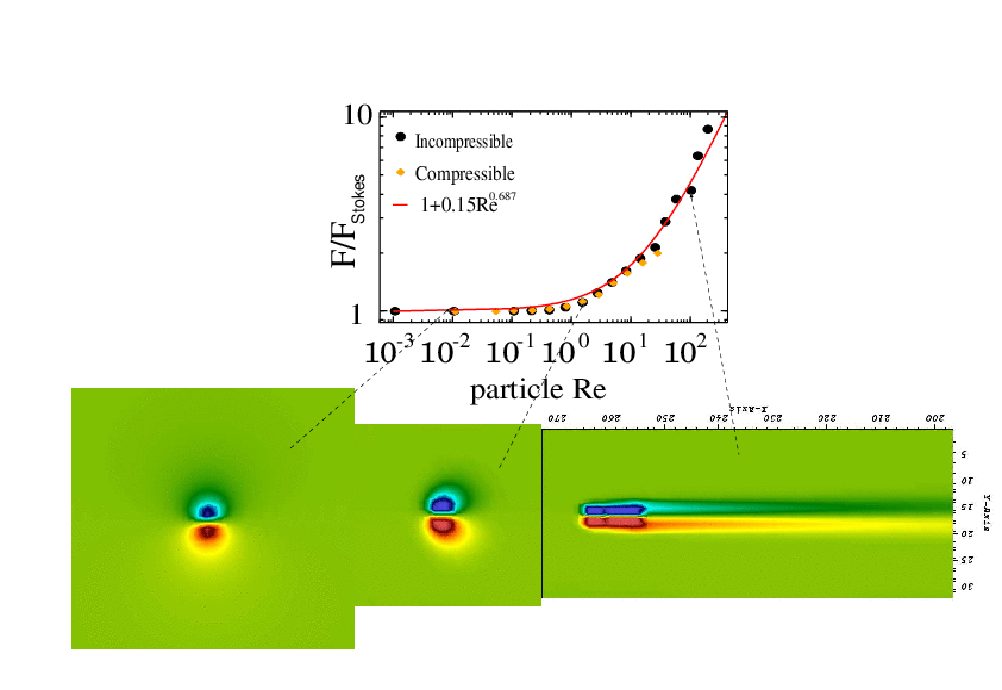 Fluid drag .vs. Reynolds number and vorticity field
around the blob particle model.
The blob model behaviour closely resembles a rigid particle!
Fluid drag .vs. Reynolds number and vorticity field
around the blob particle model.
The blob model behaviour closely resembles a rigid particle!
FLUAM code
Florencio Balboa has developed a code written in CUDA, which works nicely and extremely fast in GPU cards. It can be downloaded at https://code.google.com/p/fluam
Ultrasound acoustic forcing
A standing pressure wave of about 1GHz carries micron-size
colloidal particles to the nodes of the wave
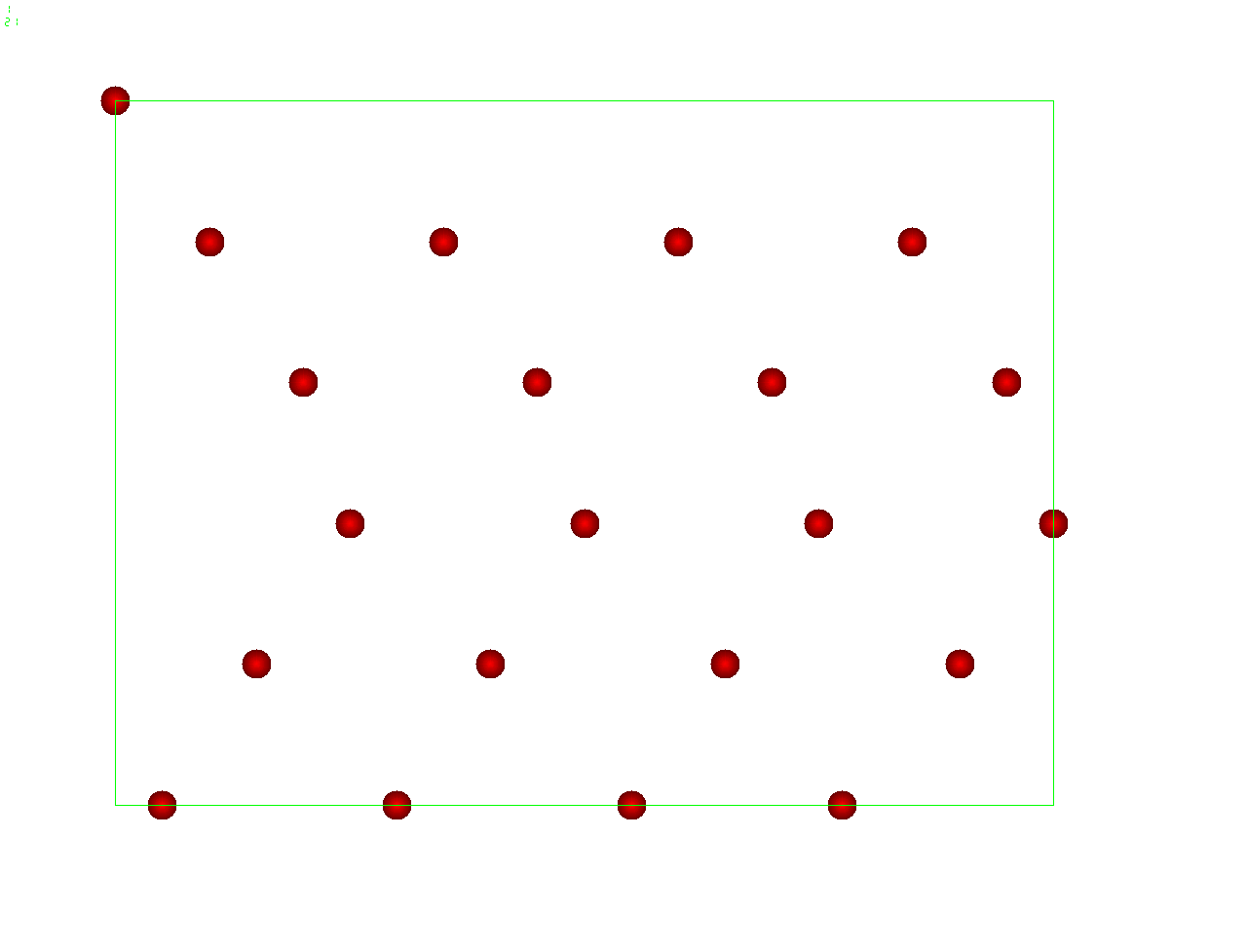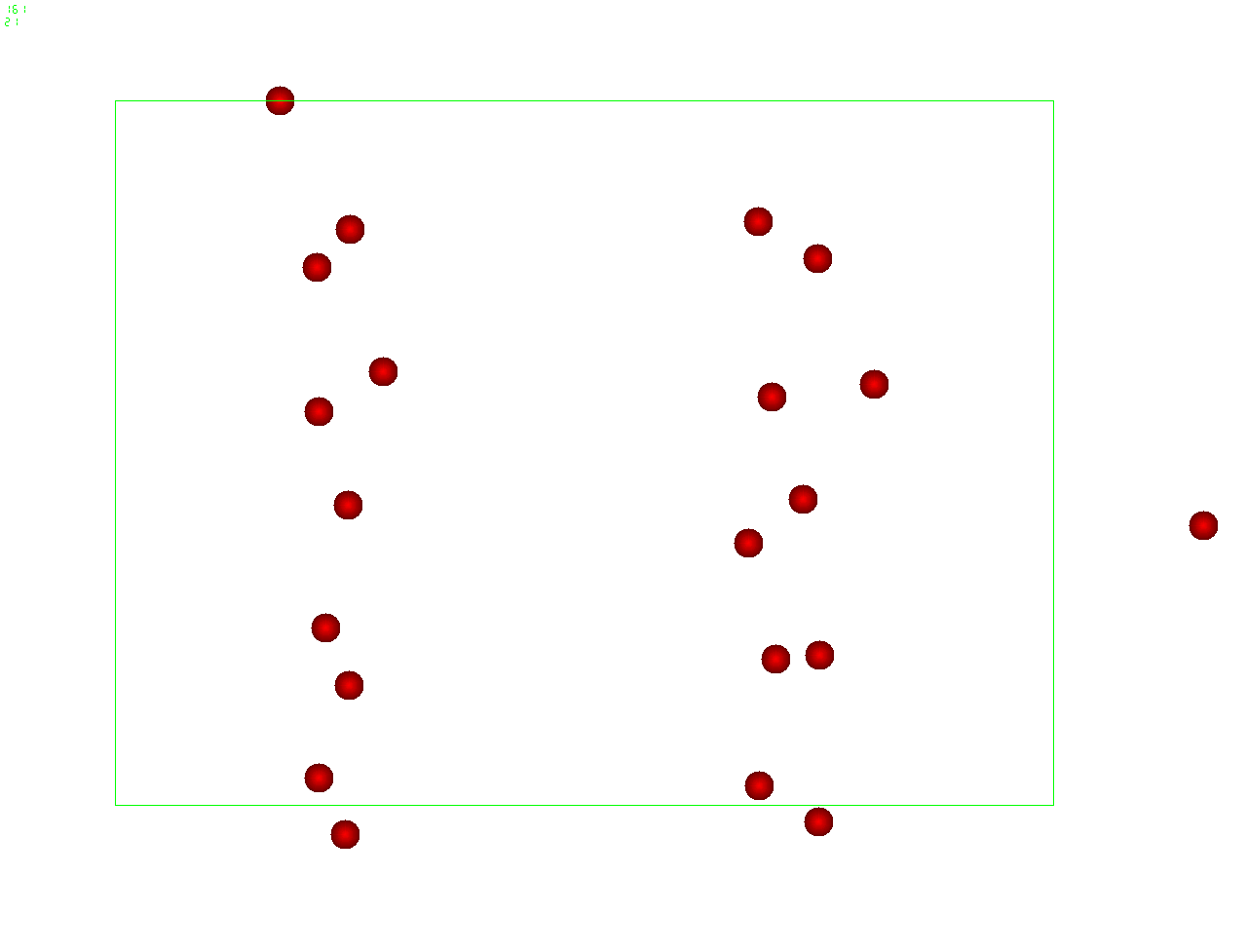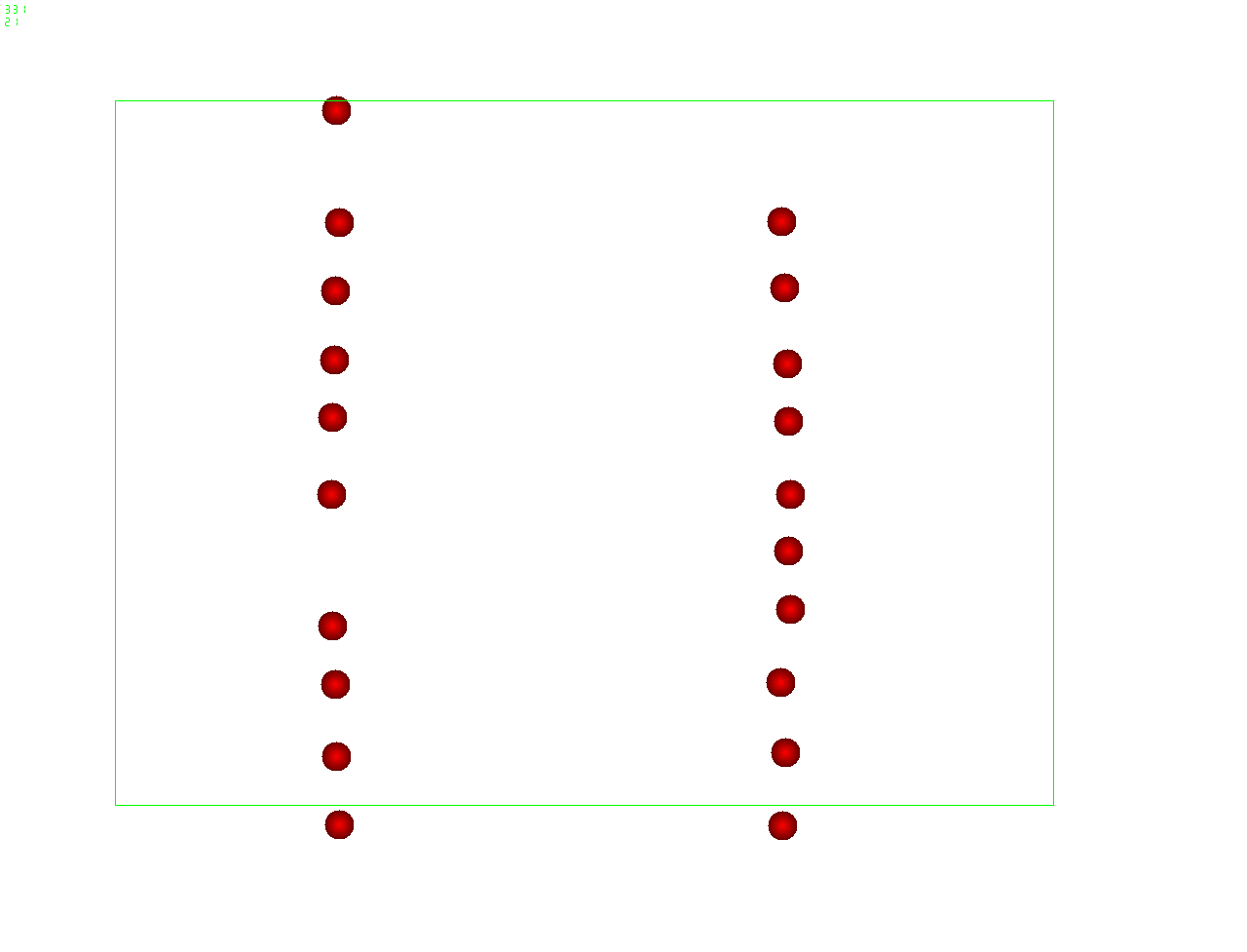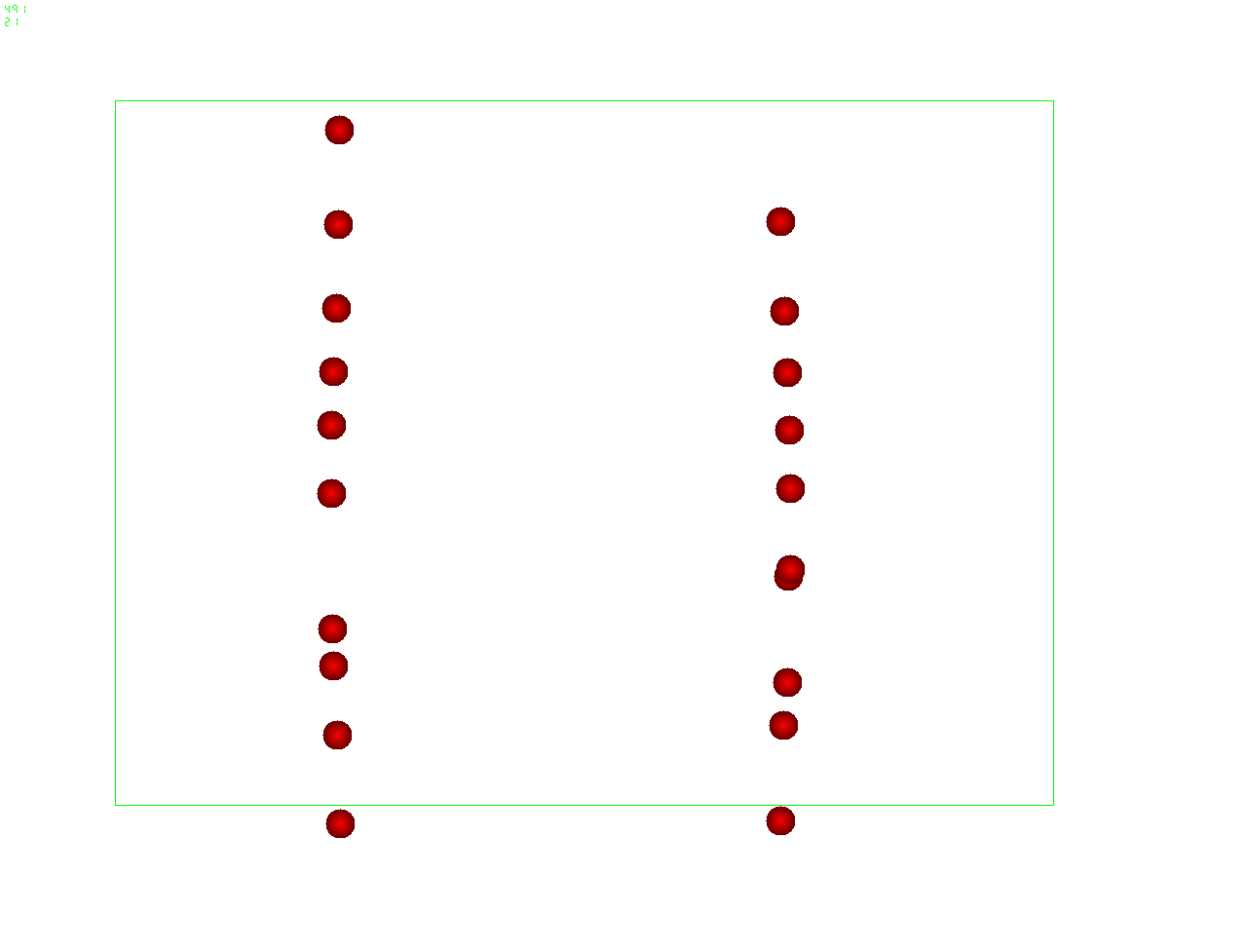

Inertial Coupling Method: Ultrasound - soft matter interaction
Recent publications
Selected talks
Coworkers
Florencio Balboa Usabiaga (UAM)
Aleks Donev (Courant Institute of New York) ,
Ignacio Pagonabarraga (Universidad de Barcelona)